Resonance can occur when there is a periodic external driving force causing a system to oscillate. When the frequency of the driving force gets closer to the natural frequency of the system, it begins to vibrate with a much greater amplitude, which continues to increase up to a maximum when the two frequencies are equal.

Factors leading to resonance

There are several factors that lead to resonance, as we shall explore below.

Natural frequency

Every object has its own natural vibration frequency. This means that if you pushed or moved the object without any other forces acting on it, it would naturally start to vibrate. If we take a mass-spring system as an example, we can see this in action. If you pull the mass away from its resting position on the spring and let it go, it will start to vibrate at its natural frequency. If there were no forces acting against the mass, it would continue to vibrate at this frequency forever! But in real life, things like air resistance always slow it down eventually.

‍

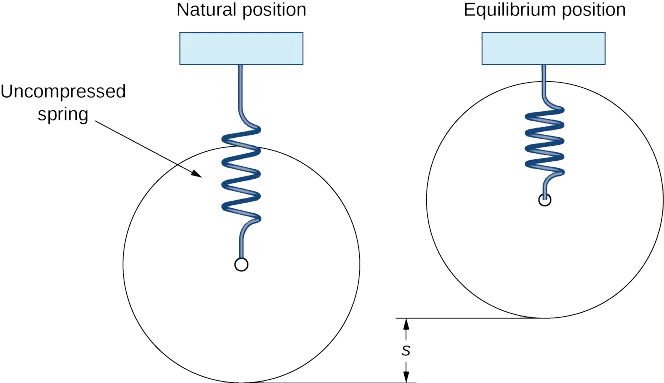
Forced vibrations

When an outside force makes something vibrate, it's called forced vibration. This force has a frequency, which we call the driving frequency. If the driving frequency matches the natural frequency of the object, it starts to vibrate much more intensely - this is resonance.

For example, a swing in a playground can be made to resonate by someone pushing it at just the right time. If the pushing happens at the same frequency as the swing's natural frequency, the swings become much higher.

Let's say a child is on a swing and their parent is pushing them every 2 seconds. The swings are getting really high because they're resonating! The frequency of the pushes is 0.5 Hz. To make this work, the parent should push when the swing is in the middle position. This happens every 0.5 seconds.

Phase difference

It is clear from the previous example that if the person pushes the swing at the wrong time, for instance, when the swing is travelling towards them, the system will not resonate. To increase the height of the oscillations, the most force should be applied when the swing is travelling away from the person pushing it and passing through the equilibrium position, which is when its speed is greatest. The time taken for the swing to move between the highest point and the equilibrium position is equal to a quarter of the overall time period, and so this needs to be the difference in time between when the swing is at maximum displacement and when the force is applied.

At higher and lower values of the driving frequency, compared to the natural frequency of the object being acted on, energy is transferred to the system much less efficiently, and the amplitude is much lower.

At low driving frequencies, the force oscillates much more slowly than the object, and there is a phase difference of 0 between them.At resonance, the phase difference is , which causes the greatest transfer of energy, as the force is always acting in the same direction as the motion, and the force is largest when the object is passing through equilibrium with maximum velocity. This is also called velocity resonance – the graphs for the driving force and the velocity of the oscillator have the same shape.When the driving frequency continues to increase past the point of resonance, the phase difference increases to π, and the force gets completely out of phase with the oscillator. At this point, the oscillator is unable to keep up with the driving force.

‍

Damping

In reality, oscillating systems can't vibrate forever because they lose energy to their surroundings. This happens because of damping forces, which are basically frictional forces that slow things down. Examples of damping forces include air resistance and the friction between moving parts of a system. These forces act to decrease the amplitude of oscillations, which means they make the oscillations smaller over time. This damping effect is important because it minimizes the effect of resonance, which can cause problems if a system vibrates too much.

The effects of different types of damping on amplitude

Light damping: the object takes a long time to stop. An example of this is air resistance acting on a swinging pendulum to slowly decrease the amplitude of the oscillations.

‍

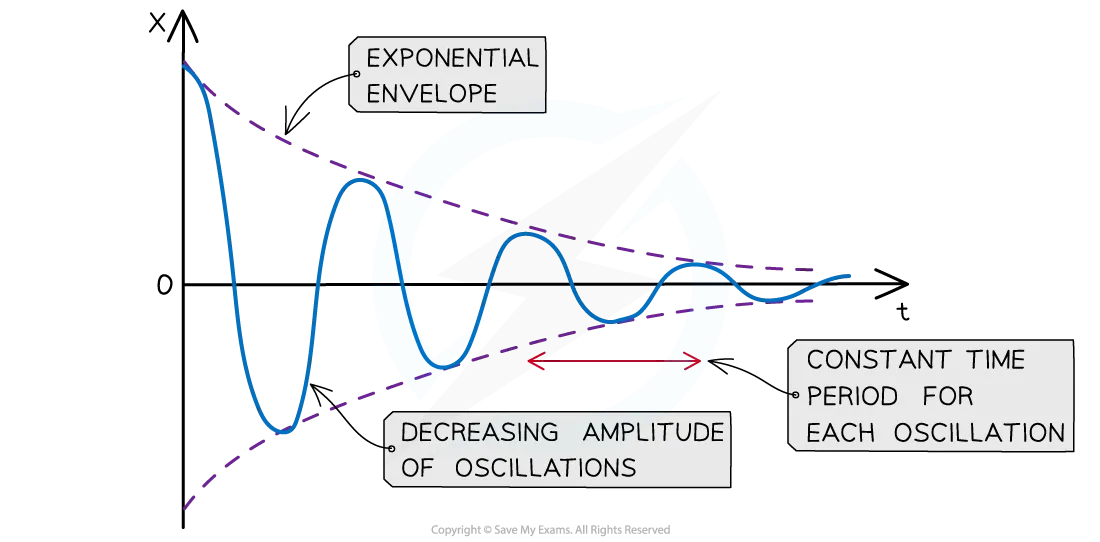
There are different types of damping that can affect an oscillating system:

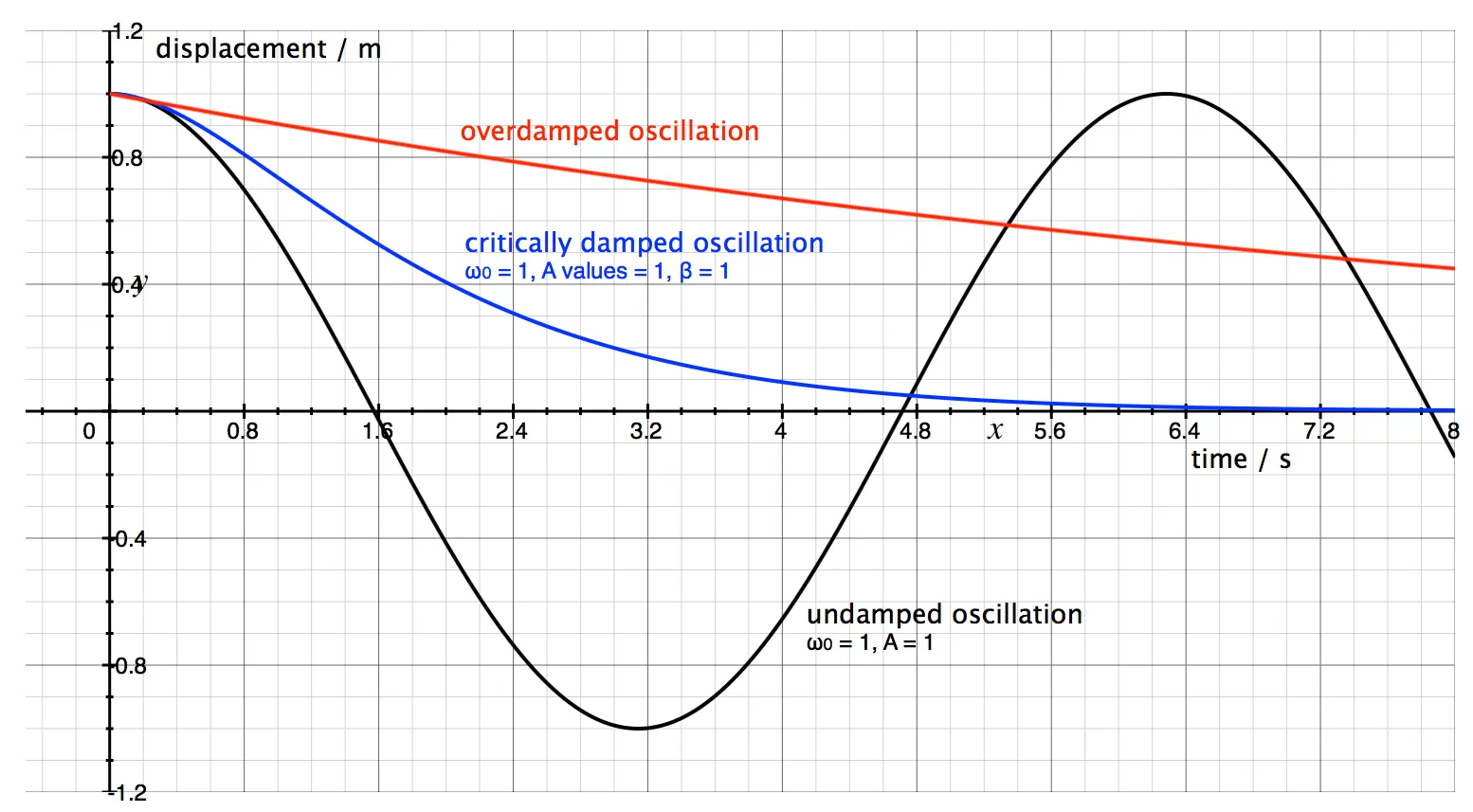
1. Heavy damping: In this case, a large force is applied against the motion of the vibrating object. As a result, it takes much less time to stop the oscillations, and the amplitude decreases greatly during each period. The graph for displacement against time would have a similar shape to the graph for light damping but would decrease to zero much more quickly. An example of heavy damping would be using an object with a very large surface area in place of the bob on a simple pendulum. The air resistance would be much greater and would decrease the amplitude more quickly.
2. Critical damping: This is the exact amount of resistive force needed to stop a system oscillating in the shortest possible time. It's the ideal amount of damping for a system because it minimizes the time it takes for the oscillations to stop.
3. Overdamping: Overdamped systems have a resistive force acting on them than critically damped ones, but take longer to return to their equilibrium. Overdamping is used for very large, heavy doors to get them to close slowly instead of slamming shut.

‍

‍

The effects of damping on resonance

Damping a of resonance on oscillating systems. Lightly damped systems have a very sharp peak in amplitude at resonance, making them very sensitive to when the resonant frequency is reached. However, as damping forces are increased, the peak of the resonance curve flattens, and the peak begins to occur slightly before resonance, causing the resonant frequency to decrease.

Damping effects can be very useful in preventing resonance-related problems in large structures, such as bridges. For example, people and objects moving over the bridge can cause it to vibrate slightly, and if the frequency matches the natural frequency of the bridge, it can oscillate violently and even break apart. By designing the bridge to have more friction between the parts that would move, the amplitude of the oscillations can be reduced, thus preventing resonance-related issues.

Applications of resonance

Although resonance can be a source of danger, it also plays an important role in many useful applications, including, for instance, MRI scans and musical instruments.

MRI scans

MRI scans are based on the effect of nuclear magnetic resonance (NMR). Hydrogen nuclei have their own natural frequency, and if a very strong magnetic field is applied to one, it can absorb energy from electromagnetic radiation (in the radio frequency range) that is equal to this frequency. The controlled de-excitation of the hydrogen nuclei enables them to be located based on the radiation they emit, which allows for the body tissue to be mapped.

‍

Musical instruments

Resonance is also essential in musical instruments. When a guitar string is plucked, a wave is produced, and the superposition of that wave forms a stationary wave on the string, which determines its pitch. However, the strings themselves would only produce a quiet sound as they easily move through the air, causing little vibration of air molecules. To produce a louder sound, the vibrations of the strings are transferred to the whole guitar body by the bridge at the end of the strings.

The guitar body is designed to have the same resonant frequencies as the frequencies of the stationary waves on the strings. This means that the guitar resonates when it is plucked, causing the surrounding air molecules to vibrate enough to produce a louder sound. This is true for most musical instruments, where resonance plays a crucial role in the production of sound.

Resonance is characterized by the oscillations of large amplitude that occur when a system is driven by a periodic force at its natural frequency. At resonance, the phase difference between the driver and the oscillator is zero. However, damping decreases the maximum amplitude of resonance and causes the resonance frequency to decrease as well. Understanding resonance is crucial in many fields including physics, engineering, and music.

Resonance

What is resonance?

Resonance describes the oscillations of very large amplitude that happen when a system is driven by a periodic force at the natural frequency of the system.

What is resonant frequency?

Resonant frequency is the driving frequency at which a system resonates.

Why is resonance a problem?

Resonance can be a problem in large structures when caused by oscillations, as it can cause the structures to break apart.

What is an example of resonance?

A child being pushed on the swing at the right moments.

‍