We talk about bodies, we refer to different properties like weight, charge, and density. Weight is connected to mass and gravity. Sometimes we can simplify things by concentrating the mass into a single point. But, when we're dealing with bigger or irregular bodies, we need a different method. That's where the Centre of Mass comes in handy. It helps us simplify the calculations for such bodies.

What is the centre of mass?

The Centre of Mass is where we assume all the mass in a body is concentrated. This concept helps us simplify problems in two ways. Firstly, it gives us a reference point to study how forces interact with the body. Secondly, it makes it easier to track the movement of the body by using the Centre of Mass trajectory.

Forces

When using the centre of mass to study body-force interactions, the forces do not act at the contact point but rather on the centre of mass.

‍

By concentrating all forces in the centre of mass, the laws of Newton and force superposition can be used to find the net force, the acceleration, and other variables.

Movement

If the forces acting on an object cause movement, this can be simplified to its centre of mass moving. In these cases, the centre of mass can be analysed using Newton’s laws on the centre of mass or the kinematic equations to obtain its displacement, velocity, and acceleration.

‍

Centre of mass of a square or rectangle

Some Centre of Masses are easier to determine than others, depending on the object's density, shape, and thickness. For example, let's say we want to find the Centre of Mass of a regular and symmetrical object like a square. If you've ever played with a square piece of metal or wood, you may have noticed that you can balance it on your finger by placing it at the centre of the square.

‍

The balancing is possible because the square has a uniform density, which means that its weight is the same at every point. The force pulling it down (gravity) is also equal in all places.The centre of mass for regular objects, such as a square, a rectangle, a circle, or an equilateral triangle, is at the centre of the geometrical shape, as shown below:

For many regular figures, their centre of mass overlaps with a geometrical point known as their centroid. The centroid is the centre of a geometrical shape.

Centroids

When an object’s density and shape are regular, the centre of mass is found at its geometrical centre or centroid, which is found in any regular 2D or 3D objects, such as spheres, cubes, and rings.

‍

Centre of a system of particles

The Centre of Mass can also be defined for a system consisting of multiple particles, such as when analyzing charges or point masses. If the objects have a regular density, we can use the following formula to find the Centre of Mass:

R = (m1r1 + m2r2 + m3r3 + ... + mn rn) / (m1 + m2 + m3 + ... + mn)

Here, the vectors r represent the coordinates x, y, and z measured from the origin. This formula can be broken down into three separate formulas for the x, y, and z positions as follows:

Xcm = (m1x1 + m2x2 + m3x3 + ... + mn xn) / (m1 + m2 + m3 + ... + mn)
Ycm = (m1y1 + m2y2 + m3y3 + ... + mn yn) / (m1 + m2 + m3 + ... + mn)
Zcm = (m1z1 + m2z2 + m3z3 + ... + mn zn) / (m1 + m2 + m3 + ... + mn)

Let's look at an example to see how this works. Consider a system of three particles with the configuration shown in the image below. The particles are connected by forces that keep them locked in a triangular position, and another force makes them move along the y-axis. If their individual masses are m1 = 100 g, m2 = 50 g, and m3 = 64 g, we can find the Centre of Mass that will simplify their movement.

To find the Centre of Mass, we need to calculate the x, y, and z positions for each particle and then use these values in the formulas above. Let's assume that the origin is located at the bottom left corner of the triangle, and the y-axis is pointing upwards.

Particle 1 is located at (0, 0, 0), so its x, y, and z positions are all zero. Particle 2 is located at (0.05 m, 0.03 m, 0), so its x-position is 0.05 m, its y-position is 0.03 m, and its z-position is zero. Particle 3 is located at (0.1 m, 0, 0), so its x-position is 0.1 m, its y-position is zero, and its z-position is zero.

Using the formulas above, we can find the Centre of Mass as follows:

Xcm = (m1x1 + m2x2 + m3x3) / (m1 + m2 + m3) = (1000 + 500.05 + 640.1) / (100 + 50 + 64) = 0.072 m
Ycm = (m1y1 + m2y2 + m3y3) / (m1 + m2 + m3) = (1000 + 500.03 + 640) / (100 + 50 + 64) = 0.022 m
Zcm = (m1z1 + m2z2 + m3z3) / (m1 + m2 + m3) = (1000 + 500 + 64*0) / (100 + 50 + 64) = 0

Therefore, the Centre of Mass for this system is located at (0.072 m, 0.022 m, 0), which is the point where the system's overall mass can be assumed to be concentrated.

‍

‍

First, you need to obtain the coordinate of each particle in the system. In this case, the particles lie along the position y=0. The problem will be simplified to find the coordinates in x and z.You can then simplify the movement of the three particles as a single point in motion along the z and x-axes with the coordinates given below.

‍

The concept of the Centre of Gravity is helpful in simplifying analyses of the forces acting on a single body or a system of connected bodies. It is the point where the force of gravity acts in a body or system of bodies.

For objects with uniform mass, such as circles, squares, or rings, the coordinates of their Centre of Mass are given by their centroids. Once we have obtained the centroid coordinates (x, y), we can use them to find the Centre of Mass of the entire system.

In cases where the body is in motion or rotation, the Centre of Gravity still applies. For example, a billiard ball can be considered a sphere with uniform density, and both its centroid and Centre of Mass coincide in the middle. When the ball is impacted by a force 'F' in the middle, it experiences the effects of gravity pulling it downwards, and friction also comes into play.

However, there are instances where the forces acting on a rotating body may not be applied at the Centre of Mass, causing torque and inducing rotation. Nonetheless, for bodies with regular density, such as a sphere, the Centre of Mass remains a useful concept to simplify force analysis.

‍

‍

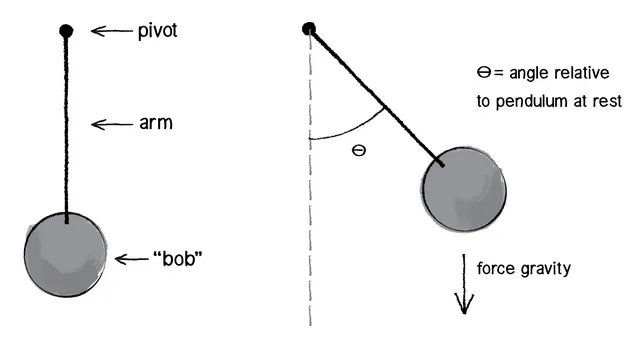
The force of friction ‘f’ acts perpendicular to the contact surface and against the movement of the ball. This force acts at a distance ‘d’ from the centre of the ball, causing a torque.

‍

The torque caused by the friction is responsible for the ball’s rotation.

Centre of gravity vs centre of mass

The centre of gravity and the centre of mass should not be confused. One depends on the mass distribution of a body, while the other depends on the force of gravity that acts on the body. Both might overlap in special cases, such as when the mass of the object is regular and the gravitational field uniform. See the following example.

1. The centre of mass depends on the mass distribution of a body, while the centre of gravity depends on the force of gravity acting on the body.
2. The centre of mass is the point where the total mass of a system is considered to be concentrated, while the centre of gravity is the point where the force of gravity acts on the body.
3. The centre of mass is a geometrical concept, while the centre of gravity is a physical concept.
4. In a uniform gravitational field, the centre of mass and the centre of gravity coincide, but in a non-uniform gravitational field, they may not.
5. The centre of mass remains constant, while the centre of gravity may change due to variations in the gravitational field.

Projectile launch

During a projectile launch in parabolic motion, the centre of mass remains stable, even if the object rotates while travelling. In this case, the object rotates around its centre of mass, describing a parabola, as shown below.

‍

In the case of the launch of a rocket or a projectile, if the object separates into two parts, the motion of the centre of mass follows the original trajectory, while the parts of the projectile follow different paths, as shown below.

Centre of Mass - Key takeaways The centre of mass is the place where we can assume all mass to be concentrated in a body. The centre of mass is useful for simplifying the forces acting on a body or its motion. The centroid is the geometrical centre of an object. The centre of mass and the centroid coincide for bodies with regular symmetry and uniform density. The centre of gravity is the geometrical place where we can assume the force of gravity to be acting on a body. The centre of gravity and the centre of mass are not the same. One distinguishing feature is that the centre of gravity depends on the force of gravity, whereas the centre of mass does not.

Centre of Mass

Are the centre of gravity and centre of mass the same?

No, the centre of gravity is the geometrical position where the gravity force acts. In contrast to the centre of mass, it depends on the force of gravity.

Can the centre of mass change in a projectile launch?

No, the centre of mass will stay the same, even if the projectile itself divides, as in the case of rockets.

What is the centre of mass?

The centre of mass is the place where all the mass is assumed to be concentrated.

‍