Have you ever wondered why a sharp knife can slice through fruit like butter but a dull one can't? The answer lies in pressure. It's not just about how much force is used, but also how much force is applied over a certain area. In this article, we'll learn all about pressure, including how to calculate it and why it matters in our everyday lives. By the end, you'll be a pressure pro! So let's dive in.

Pressure definition

Before we get into the nitty-gritty of pressure calculations, let first understand what pressure means in physics. In simple terms, pressure is the amount of force applied to a surface per unit area. So, it's not just about how much force is used, but also how that force is spread out over a surface. For example, when using a knife to cut fruit, the pressure from the sharp edge is concentrated over a smaller area, making it easier to cut. But if the blade is dull, the pressure is spread out over a larger area, making it harder to cut. So, let's keep this in mind as we move on to calculating pressure.

Pressure formula

Now, let's get to the math behind pressure calculations. Pressure is simply the force divided by the area over which it's applied. This can be written as:

Pressure = Force / Area

In this equation, pressure is measured in Pascals (), force is measured in units of, and area is measured in units of. For example, a pressure of 1 Pa can be defined as a force of 1 N acting on an area of 1 m². It's important to note that this formula is only valid when the force acts at a right angle to the surface.

The equation tells us that pressure is directly proportional to the force applied and inversely proportional to the area over which it's applied. So, to increase pressure, we can either increase the force while keeping the area constant, or decrease the area while keeping the force constant. Understanding this equation is key to understanding the importance of pressure in our daily lives.

‍

‍

Units of pressure

Now that we know how to calculate pressure, let's talk about the units used to measure it. The SI unit of pressure is the Pascal, which is equal to one Newton per square meter (). However, for larger quantities of pressure, we often use kilopascals () or megapascals ().

There are also other units of pressure that you may come across, such as torr, which is commonly used in the field of medicine. One torr is equal to 1/760th of standard atmospheric pressure.

Speaking of atmospheric pressure, this is a common unit of pressure that we encounter in our daily lives. Atmospheric pressure is the pressure exerted by the Earth's atmosphere on the surface of the Earth. At sea level, the atmospheric pressure is approximately 101,325 Pa or 101.325 kPa. This is sometimes referred to as standard atmospheric pressure. Understanding these different units of pressure is crucial in many fields, from engineering to medicine to meteorology.

Types of pressure

That's absolutely correct! Pressure can be exerted by solids, liquids, and gases. When a solid exerts pressure, it does so through its point of contact with another solid. For example, when you hammer a nail into a wall, the force of the hammer is concentrated onto the small point of the nail, leading to a high pressure that allows the nail to penetrate the wall.

Liquids and gases, on the other hand, exert pressure on a solid due to the collision of their particles with the solid. When a liquid or gas is in contact with a solid surface, the particles of the liquid or gas collide with the solid surface, creating a force per unit area that we perceive as pressure. This is why we feel the force of the atmosphere on our bodies, which is nothing more than the pressure exerted by the gases in the atmosphere. Understanding how pressure is exerted by different types of materials is important in many areas of science and engineering, from construction to aerospace to medicine.

The pressure exerted by liquids

You are absolutely right! The pressure exerted by liquids is primarily due to the weight of the liquid. When you dive into a pool, for example, the weight of the water directly above you exerts a force on your body, creating the sensation of pressure. This is why the pressure exerted by liquids increases with increasing depth, as the weight of the liquid above you increases.

The density of the liquid also plays a role in determining the pressure exerted. Density is the measure of mass per unit volume of a liquid. Liquids with higher densities will exert a larger pressure at the same depth because they have a greater weight per unit volume.

Understanding the pressure exerted by liquids is important in many fields, from civil engineering to oceanography to scuba diving. It's fascinating how the weight and density of a liquid can affect the pressure exerted on objects submerged in it, and this knowledge can help us design structures and equipment that can withstand the forces exerted by liquids.

‍

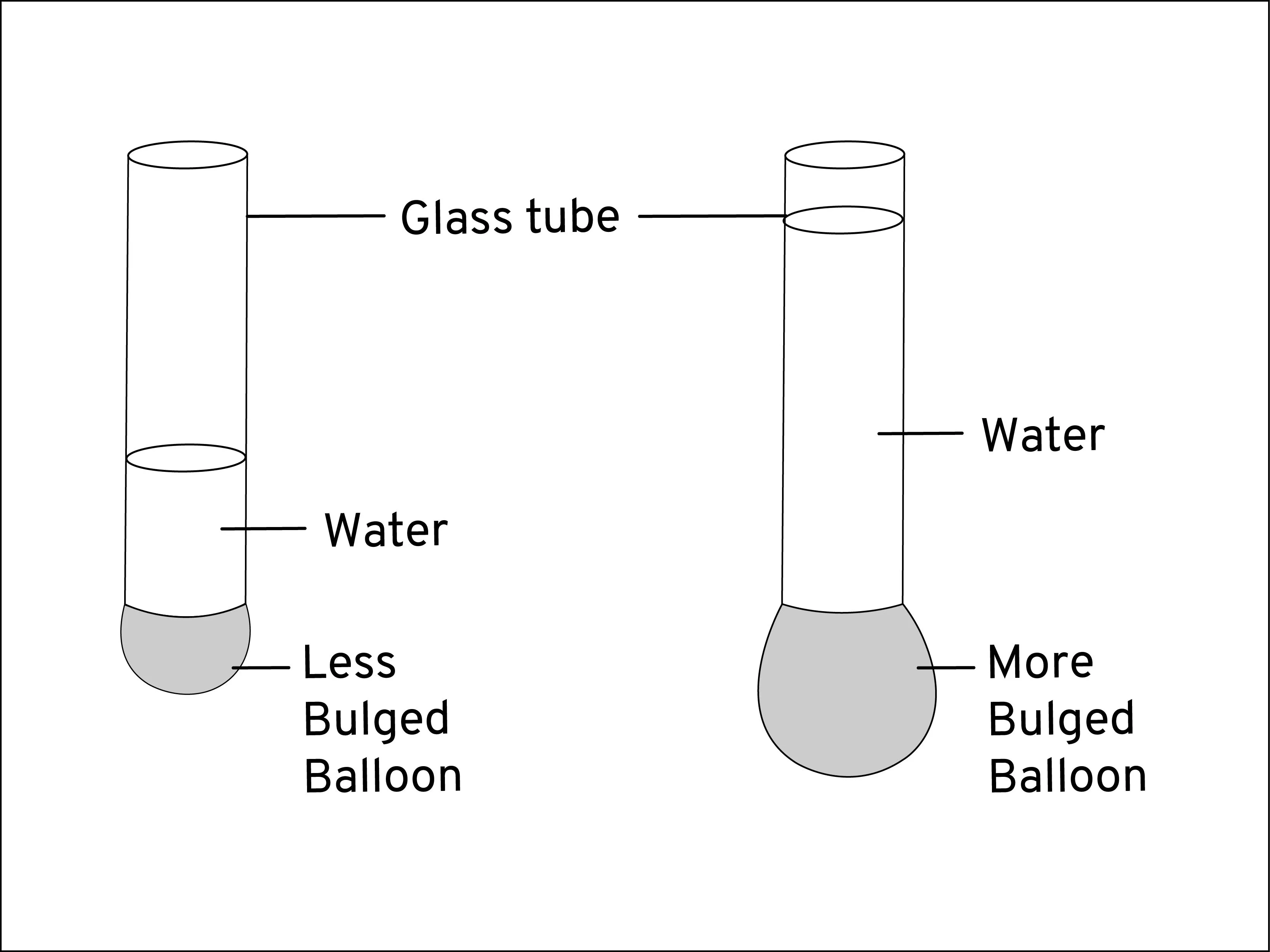
That's a great explanation of how to calculate the pressure exerted by a liquid at a particular depth! Let's take a look at a few examples of how to use these formulas in practice:

Example 1: A rectangular fish tank has a length of 1 meter, a width of 0.5 meters, and a height of 0.75 The tank is filled with water to a height of 0.6 meters. Calculate the pressure exerted by the water at the bottom of the tank.

First, we need to calculate the base area of the tank:

Base area = length x width = 1 m x 0.5 m = 0.5 m^2

Next, we need to calculate the height of the column of water:

Height = 0.75 m - 0.6 m = 0.15 m

The density of water is 1000 kg/m^3, and the gravitational field strength is 9.81 m/s^2. Using the formula for pressure, we can calculate:

Pressure = density x gravity x depth
Pressure = 1000 kg/m^3 x 9.81 m/s^2 x 0.15 m
Pressure = 1471.5 Pa

Therefore, the pressure exerted by the water at the bottom of the tank is 1471.5 Pa.

Example 2: A swimming pool has a length of 20 meters, a width of 10 meters, and a depth of 2 meters. Calculate the pressure exerted by the water at the bottom of the pool.

First, we need to calculate the base area of the pool:

Base area = length x width = 20 m x 10 m = 200 m^2

Next, we need to calculate the height of the column of water:

Height = 2 m

The density of water is 1000 kg/m^3, and the gravitational field strength is 9.81 m/s^2. Using the formula for pressure, we can calculate:

Pressure = density x gravity x depth
Pressure = 1000 kg/m^3 x 9.81 m/s^2 x 2 m
Pressure = 19620 Pa

Therefore, the pressure exerted by the water at the bottom of the pool is 19620 Pa.

Atmospheric pressure

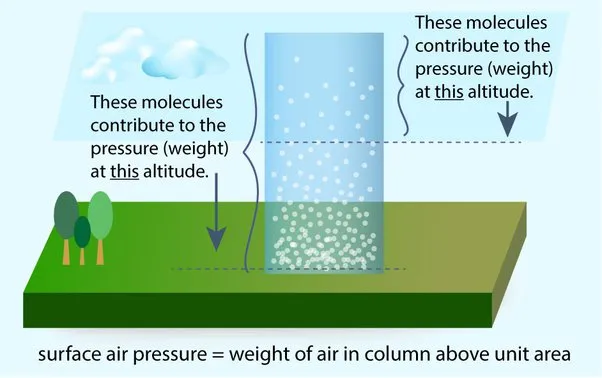
Atmospheric pressure is due to the weight of the air pressing down on the earth or any other object contained within the atmosphere. As you mentioned, this pressure decreases as the altitude increases because the density of the air decreases at higher altitudes. This is why many people experience ear pain during air travel or when traveling to high-altitude locations such as mountains. When there is a quick change in air pressure, such as during takeoff or landing of an airplane, the pressure inside the ear can become imbalanced, causing discomfort.

The formula for calculating atmospheric pressure is the same as the formula for calculating the pressure due to liquids. It is given by:

Pressure = density x gravity x height

Where density is the density of air, gravity is the gravitational field strength, and height is the altitude or height above sea level. However, because the density of air varies with altitude, the pressure at a particular altitude is not constant and must be calculated using atmospheric models or measured with specialized instruments.

Understanding atmospheric pressure is important in fields such as meteorology, aviation, and engineering, where changes in air pressure can have significant effects on the performance and safety of equipment and structures.

‍

‍

‍

Examples of pressure

Sure, let's calculate the pressure in the first part of your question:
Given:
Weight of fluid = w = 200 N
Surface area = A = 0.5 m^2

The formula for pressure is:

Pressure = Force / Area

In this case, the force is the weight of the fluid, so we can substitute:

Pressure = w / A
Pressure = 200 N / 0.5 m^2
Pressure = 400 Pa

Therefore, the pressure acting on the surface is 400 Pa.

Now, let's move on to the second part of your question:
Given:
Weight of person = w = 600 N
Contact area of flat shoe = A1 = 0.01 m^2
Total contact area of heeled shoe = A2 = 0.02 m^2

To calculate the pressure exerted on the ground by the person wearing the flat shoe, we can use the same formula:

Pressure = Force / Area

In this case, the force is the weight of the person, so we can substitute:

Pressure = w / A1
Pressure = 600 N / 0.01 m^2
Pressure = 60000 Pa

Therefore, the pressure exerted on the ground by the person wearing the flat shoe is 60000 Pa.

To calculate the pressure exerted on the ground by the person wearing the heeled shoe, we can use the same formula:

Pressure = Force / Area

In this case, the total contact area of the heeled shoe is used:

Pressure = w / A2
Pressure = 600 N / 0.02 m^2
Pressure = 30000 Pa

Therefore, the pressure exerted on the ground by the person wearing the heeled shoe is 30000 Pa.

What can you infer from the results?

‍

Sure, I can help with the unit conversions and calculations.

For the pressure on the ground due to flat shoes:
Pressure = 60000 Pa
To convert to pounds per square inch (psi), we can use the conversion factor 1 psi = 6894.76 Pa:

Pressure = 60000 Pa / 4.76 Pa/psi
Pressure 8.7 psi (approximately)

For the pressure on the ground due to heels:
Pressure = 30000 Pa
To convert to psi:

Pressure = 30000 Pa / 6894.76 Pa/psi
Pressure = 4.35 psi (approximately)

As you mentioned, the pressure exerted by the heels is almost 5 times that of the flat sole shoes.

Next, let's calculate the pressure in the water well:
Given:
Depth = 10 m
Density of water = 1000 kg/m^3
Acceleration due to gravity = 9.81 m/s^2

The formula for pressure at a depth in a fluid is:

Pressure = density x gravity x depth

Substituting the given values, we get:

Pressure = 1000 kg/m^3 x 9.81 m/s^2 x 10 m
Pressure = 98100 Pa

Therefore, the pressure in the water well at a depth of 10 m is 98100 Pa.

Finally, let's calculate the density of air at an altitude of 2000 m where the pressure of the surrounding atmosphere is 80 kPa:
Given:
Altitude = 2000 m
Pressure = 80 kPa = 80000 Pa

To calculate the density of air, we can use the ideal gas law:

PV = nRT

where P is the pressure, V is the volume, n is the number of moles of gas, R is the universal gas constant, and T is the temperature.

Assuming that the temperature is constant and using the molar mass of air28.97 g/mol), we can rearrange the equation to solve for density:

density = (P x M) / (R x T)

where M is the molar mass of air.

Substituting the given values, we get:

density = (80000 Pa x 0.02897 kg/mol) / (8.314 J/mol·K x 288 K)
density = 1.12 kg/m^3

Therefore, the density of air at an altitude of 2000 m where the pressure of the surrounding atmosphere is 80 kPa is 1.12 kg/m^3.

Pressure - Key takeaways

That is correct! Pressure is the force exerted per unit area, and it can be calculated by dividing the force by the area across which it is acting. The pressure exerted by a liquid increases with depth due to the weight of the liquid above it. Similarly, atmospheric pressure is due to the weight of the air molecules on top of the earth, and it reduces as the altitude increases since there are fewer air molecules above.

Pressure

What is pressure?

Pressure is defined as the force per unit area.

How do you calculate pressure?

The formula for pressure is P=F/A

What is the formula for pressure?

The formula for pressure is P=F/A

What is an example of pressure?

A knife cutting a slab of butter, A nail being hammered into a wall are examples of pressure

What are the types of pressure?

The types of pressure are Absolute pressure. Gauge pressure. Differential pressure. Sealed pressure or vacuum pressure.

‍