Half life is a way to measure how long it takes for a radioactive sample to lose half of its mass or quantity. This helps us understand how dangerous the substance can be. But, half life isn't just important for understanding radioactive materials. It's also useful for carbon-14 dating techniques and other applications. So, while it's important to be aware of the risks of radioactive materials, studying half life can help us learn more about the world around us. Keywords: Half life, radioactive sample, decrease, carbon-14 dating techniques, danger.

What is nuclear decay?

Certain elements in nature contain atoms with an excess of particles or energy, which makes them unstable. These unstable atoms emit particles to try and become stable again. This process is called nuclear decay, or radioactive decay. It's a quantum effect that occurs with a certain probability. This means we can only predict the likelihood of a certain decay happening over a certain period. For example, if we predict that 90% of a sample's nuclei will decay after one day, it could happen in one second or one week. However, if we have a lot of identical nuclei, 90% of them will have decayed after one day. The general equation that models this effect includes variables such as N(t) (the number of unstable nuclei at time t) and λ (the decay constant, which is specific to each decay process). For more information, check out our article on Radioactive Decay. Keywords: elements, unstable, quantum effect, radioactive decay, decay constant, probability, sample.

What is half life?

Half life is the time it takes for a sample of an unstable isotope to reduce its number of unstable nuclei by half. This might seem counterintuitive at first, since we expect a constant rate of change. But in nuclear decay, this isn't the case. The equation shows that the rate of decay isn't constant, and that's why we use the concept of half life to measure it. Instead of a fixed amount of unstable nuclei decaying in a certain period, we have a probability of certain nuclei decaying over a certain period. This makes the concept of half life crucial in understanding nuclear decay. Keywords: half life, unstable isotope, nuclei, decay, constant rate, probability.

The half life symbol and half life equation

Suppose we examine a sample at time t1 and then at a later time t2. We can find the ratio of the number of unstable atoms in the sample by dividing their expressions. This ratio is independent of the initial number of unstable nuclei. The decay constant for a specific element is known, so we know that the number of unstable nuclei will decrease in the same percentage (ratio) for a specific time interval. The percentage decrease of unstable nuclei is constant for a fixed interval, but the decrease is faster at earlier times because the total number of unstable nuclei is bigger. These facts are crucial in understanding how nuclear decay works. Keywords: sample, unstable atoms, ratio, decay constant, time interval, percentage decrease.

‍

‍

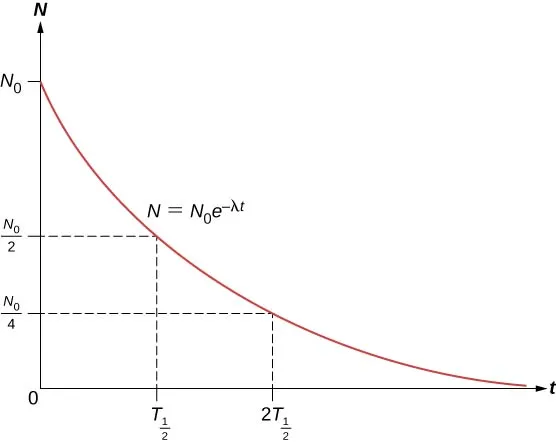
When we divide the number of unstable atoms at different times for a fixed interval, we obtain the same quantity, which reflects the constant percentual decrease of the number of unstable nuclei. This decrease is faster at earlier times, leading to a decrease in the total number of unstable atoms in the sample. This is why radioactive samples become less dangerous over time. The half-life of an isotope is the time it takes for a sample to lose half of its unstable nuclei and depends only on the isotope's decay constant, not the initial number of unstable nuclei. Some isotopes have a very short half life, while others have a very long half life, making them dangerous. This information is crucial in understanding the properties and effects of radioactive isotopes. Keywords: unstable atoms, percentual decrease, total number, radioactive samples, half-life, decay constant, isotopes.

What are some applications of half life?

Half life is a valuable indicator of the age of a sample or the needed containment time of a particular material. Let’s look at this in more detail.

Carbon-14 dating techniques

Carbon plays an essential role in the functioning of organic beings, as it is the basis of all life on Earth. Carbon-12 and carbon-13 isotopes, while carbon- is an unstable isotope. Carbon-12 is the most abundant isotope, and is found in every organic structure. Carbon-14 is formed in the atmosphere due to radiation from outer space, and is used in radiocarbon dating. Radiocarbon dating is a method used to estimate the age of organic materials, such as humans and animals, by measuring the amount of carbon-14 present in the material .This method was developed by the American physicist Willard F. Libby in 1946 , and has since been used extensively in environmental sciences, archaeology, anthropology, and other related fields.

Storage of dangerous materials

The decay equation is used to calculate how long radioactive materials need to be stored so that they no longer emit large amounts of radiation. There are three types of radioactive waste: low-level waste, intermediate-level waste, and high-level waste. Low-level waste comes from hospitals and industry and emits low levels of ionizing radiation, which can still pose an environmental threat. These wastes may be shielded, incinerated, compacted, or buried shallowly. The half-life of low-level waste is typically around five years. Intermediate-level waste includes sludge, fuels, and chemical waste, and requires shielding,ification, and burial in relatively. The of intermediate-level waste ranges from five to 30 years. High-level waste includes heavy atomic elements like uranium and materials involved in nuclear fission. These products must be cooled before being subjected to deep geological burial in concrete and metal containers for a long period of time. The half-life of high-level waste is typically over 30 years. Proper disposal of radioactive waste is crucial to prevent harm to the environment and human health.

‍

‍

Tracers

Gamma emitters are commonly used as tracers because their radiation is not very dangerous and can be accurately detected by specific devices. Tracers are used to trace a substance's distribution in a medium, such as fertilizers in soil, or to explore the human body. Tracers used for medical purposes have a short half-life, which means that they do not emit radiation for a long time inside the body and cause damage.

Decay calculations are also used to determine if a radioisotopic tracer is suitable for use. Tracers must be neither highly radioactive nor not radioactive enough, as radiation levels that are too high or too low would prevent the measuring devices from detecting or "tracing" them. Additionally, the half-life of a tracer is used to classify it by the rate of decay.

The half-life is the time it takes for a sample of a certain unstable isotope to halve its number of unstable nuclei. The process of unstable nuclei transforming into stable nuclei is called nuclear decay, or radioactive decay. Decay is a random process, but it is accurately described by exponential decay when considering samples with a large number of unstable nuclei. The half-life is a useful quantity with many applications, including dating techniques and the handling of radioactive waste.

Half Life

What is half life?

Half life is the time it takes a sample of a certain unstable isotope to half its number of unstable nuclei.

How do you calculate the half life?

If you know the decay constant λ, you can apply the following equation to calculate the half life: τ = ln (2)/λ.

What is the half life of a radioactive isotope?

The half life of a radioactive isotope is the time it takes a sample of a certain unstable isotope to half its number of unstable nuclei.

How do you find the half life from a graph?

By looking at a graph of radioactive exponential decay, you can find the half life by simply looking at the time interval passed where the number of unstable nuclei has decreased in half.

How do you find the half life given the decay rate?

If you know the decay constant λ, you can apply the following equation to calculate the half life: τ = ln (2)/λ.

‍