Electric fields are generated by sources in the space around them. When a particle is electrically charged, it generates electric field. Both protons and electrons have electric fields, and within a certain distance, they can either attract or repel other charged particles. So, if you're interested in learning about these fascinating fields, keep reading!

Definition of electric field

Forces have direction and magnitude, just like the electric field. The electric field is measured in Newton/Coulomb or volts/m and is a vector quantity. If a positive is isolated, the electric field around it radiates outwards in all directions. On the other hand, if a negative charge is isolated, the electric field around it is directed inwards. In terms of forces, positive charges experience force in the direction of the electric field, while negative charges experience force in the opposite direction of the field. Keep reading to learn more about the fascinating properties of electric!

Coulomb’s law and the field of a charge

The simplest electric field is created by a single charged particle. Coulomb's law can be used to calculate the force between two particles (q and qi) at a distance of r, with ri being the vector between the particles. A constant called vacuum permittivity or absolute dielectric permittivity (ε₀) with a value of 8.85x10^-12 F/m is used in this equation. If we set the charge at an intensity of 1, we can calculate the electric field of the particle qi using this equation: Here, the constant part of the formula (including the permittivity) is represented by k, which has a value of 9x10^9 kg⋅m^3⋅s^-2⋅C^-2.

The electric field is determined by the distance between the application point and the source of the field, as well as the intensity of the charge. In the case of a single particle, we can locate equipotential concentric spheres where the strength of the field is the same. By adjusting the terms, we can also use this formula to calculate more complex cases, such as multiple charges. To do this, we must consider the effect of each charge on the application point, and add up their contributions. Keep reading to learn more about electric fields and how they work!

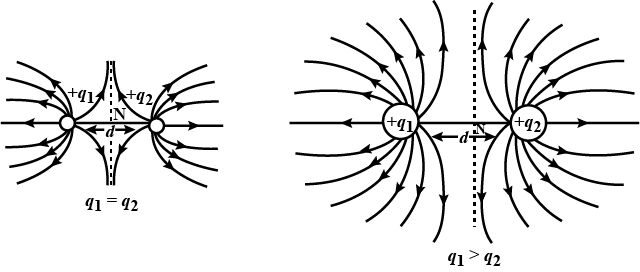
Indeed, the formula used to calculate the electric field for multiple charges is similar to that for a single charge, with the only difference being the need to add up the contributions of all the charges. In this case, N represents the total number of charges. It is important to respect the direction of each contribution when carrying out the vector sum. By doing so, we can accurately calculate the electric field at any given point. This is a fundamental concept in the study of electromagnetism and has numerous practical applications in our daily lives. Whether we are using electronics, charging our phones, or simply turning on a light switch, we are constantly interacting with electric fields. Understanding how they work and how to manipulate them is essential for advancing our technology and improving our quality of life.

The electric field of distributed charges

In some situations, it may be more useful to consider objects with a particular shape and volume instead of individual particles. In this case, we can use the superposition principle and consider a homogeneous density of charge (ρ) instead of the charge of a single particle. To calculate the electric field in this scenario, we need to perform an integral that takes into account the distribution of the charge inside the object.

It is also possible to consider a non-homogeneous density of charge, where the charge varies along one or more dimensions in space and throughout the volume. To name this density, we add the dimensions on which it depends in parentheses. For example, a density of charge that varies along the x dimension is represented by ρ(x). The calculation becomes more complex, but the concept remains the same.

By using these formulas, we can accurately calculate the electric field in a wide range of situations, from simple single-particle scenarios to complex objects with non-homogeneous density of charge. Understanding the principles behind these calculations is crucial for many fields of science and engineering, and helps us develop new technologies and solve practical problems in our daily lives.

Electric potential

In order to understand the movement of charges within an electric field, we need to use electric potential. Electric potential is the amount of energy required to move a charge within an electric field from one point to another without any loss or transformation of energy.

To define electric potential, we need a reference point. The first reference point is the source of the electric field itself. For a single particle with a test charge immersed in its field, the potential is determined by a formula that is similar to that of force, but uses the radius instead of its square power. It is important to note that electric potential is a scalar quantity, and that it depends on the test charge.

To find the potential difference (ΔV) between two points, we can take the difference between the potentials at those two points. If we move the second point very far away from the first point, the potential difference becomes more dependent on the first point and less dependent on the second point, to the point where we can ignore the second point altogether. The unit of measure for electric potential is volts.

Understanding electric potential is crucial for understanding the movement of charges within an electric field, as well as for calculating the interactions between charges within that field. By using these principles, we can better understand the behavior of electricity and develop new technologies to harness its power.

Electric Fields

What is an electric field?

A field is generated by a source in the space around it. An electric field is generated by an electrically charged particle.

Do electric currents always produce magnetic fields?

The movement of electrically charged particles generates a magnetic field.

Is electric field strength a vector?

Yes, it is.

How does moving a magnetic field create an electric field?

Through induction, as Faraday’s law states.

What creates an electric field?

An electrically charged object or a magnetic field.

‍