Momentum is a word that comes up often in sports. It describes when a team is doing well and winning games. But did you know that momentum is also a math concept in physics? This means that it can be measured and calculated. So, while we may not use the word momentum in our daily conversations, it's actually a pretty important idea in science!

What is linear momentum?

Any object with mass that is moving has momentum. In this explanation, we look at objects moving linearly. So what is linear momentum?

Linear momentum is the product of the mass and velocity of an object.

Calculating momentum

The momentum of any object depends on two things: mass and velocity. We can express it mathematically as:

In physics, momentum is represented by the letter p. The formula for momentum is p = mv, where m is mass of the object in kilograms (kg) and v is the velocity of the object in meters per second (m/s). Momentum is a vector quantity and it's measured in units of kg⋅m/s. According to the equation, if an object's velocity increases, its momentum will increase too (they have a directly proportional relationship). The more momentum an object has, the more force it will need to stop.

What is the impulse?

Let's say you're driving a car and you want to bring it to a stop. The momentum of the car depends on its mass and velocity. To stop the car, you'll need to slam on the brakes, which will apply a large deceleration force to bring the car to rest. The force required to stop the car depends on its momentum.

The force a moving object to rest is called impulse. Impulse is the change in momentum of an object when a force is applied over a certain amount of time. It's measured in Newton seconds (N·s). You can find the impulse or change in momentum by looking at the area under a force-time graph.

What is the impulse-momentum theorem?

The impulse-momentum theorem states that the change in impulse is equal to the change in momentum. We can express this mathematically as:

Impulse = Change in Momentum

If we break down the change in momentum, we get:

Impulse = mvf - mvi

Where mvf is the final momentum and mvi is the initial momentum.

The rate of change of momentum can be expressed as:

Impulse/Time = (mvf - mvi)/t

Where v is the final velocity and u is the initial velocity.

What is the law of conservation of linear momentum?

If you have two objects of masses m1 and m2 heading towards each other with velocities u1 and2, the total momentum of the system before the collision can be calculated as:

Total Initial Momentum = m1u1 + m2u2

After the collision, the two objects will have new velocities, v1 and v2. The total momentum of the system after the collision can be calculated as:

Total Final Momentum = m1v1 + m2v2

According to the law of conservation of momentum, the total momentum before and after the collision must be equal, so we can set these two equations equal to each other:

m1u1 + m2u2 = m1v1 + m2v2

We can rearrange this equation to solve for one of the velocities. For example, we can solve for v1:

v1 = [(m1 - m2)u1 + 2m2u2]/(m1 + m2)

Similarly, we can solve for v2:

v2 = [(m2 - m1)u2 + 2m1u1]/(m1 + m2)

These equations allow us to calculate the velocities of the two objects after a collision, given their masses and initial velocities.

Two objects about to collide

Both objects collide with each other after some time and exert forces F1 and F2 on each other.

‍

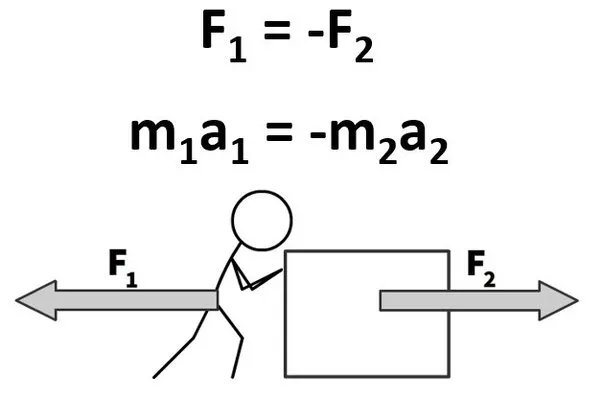
After the collision, the two objects will move in the opposite direction with velocities v1 and v2 respectively.

‍

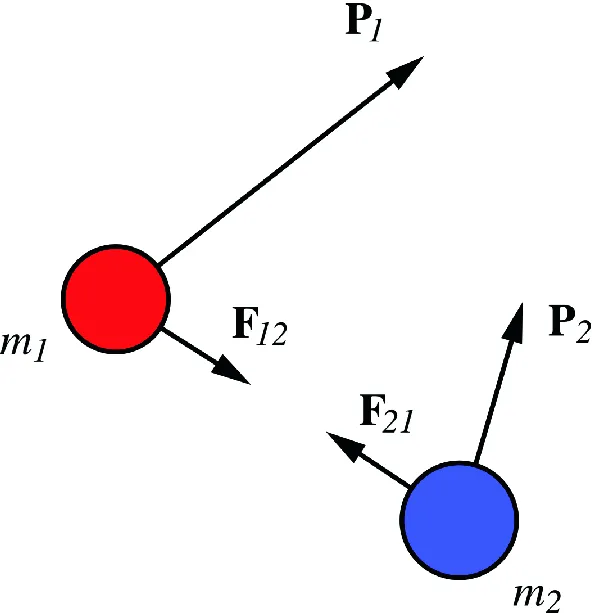
The equation you have provided is a statement of the law of conservation of linear momentum, which states that the total momentum of a closed system of objectssuch as two colliding objects) remains constant if no external forces act on the system. This means that the total momentum of the objects before the collision is equal to the total momentum of the objects after the collision.

The equation you have provided is a mathematical representation of this law, where m1 and m2 are the masses of the two objects, u1 and u2 are their initial velocities, and v1 and v2 are their final velocities. The equation shows that the product of the mass and velocity of each object before the collision is equal to the product of the mass and velocity of each object after the collision.

This equation assumes that the collision is elastic, meaning that no energy is lost during the collision. In reality, most collisions are inelastic, meaning that some energy is lost as heat or sound. In such cases, the total momentum is still conserved, but the total kinetic energy is not.

Momentum: are there different types of collisions?

In fact, there are different types of collisions, and the type of collision affects the behavior of the objects after the collision.

In an elastic collision, as I mentioned earlier, the total kinetic energy of the system is conserved, and the colliding objects move apart separately after the collision. This is the simplest type of collision that conserves momentum.

In an inelastic collision, the total kinetic energy of the system is not conserved, and the colliding objects may stick together after the collision. In this case, the momentum is still conserved, but the objects do not move apart separately after the collision.

There is also a third type of collision called a perfectly inelastic collision, where the colliding objects stick together after the collision and move together with a common velocity. In this case, the momentum is again conserved, but the objects do not move apart separately after the collision.

Regardless of the type of collision, the law of conservation of linear momentum still holds true, meaning that the total momentum of the system remains constant before and after the collision.

Collisions

A collision happens whenever an object in motion comes into contact with another object that is at rest or in motion.

Pool balls on a table. Balls on a pool table disperse after coming into collision with each other, unsplash.com

Elastic collisions

With elastic collisions, the objects that come into contact remain separate. In other words, the objects don’t combine to form a new object. The total kinetic energy and momentum are conserved in this type of collision, which is why the objects bounce off one another without the loss of any energy.

‍

When a soccer player kicks a ball, it is an example of an inelastic collision. Some of the kinetic energy of the foot is transferred to the ball, causing it to move. However, some of the kinetic energy is also lost as heat and sound, making the collision not perfectly elastic.

In nearly elastic collisions, as you mentioned, some form of energy is converted to other forms, such as heat or sound. This means that the total kinetic energy of the system is not conserved. However, the law of conservation of linear momentum still holds true, meaning that the total momentum of the system remains constant before and after the collision.

In the case of a soccer player kicking a ball, the momentum of the foot before the collision is equal and opposite to the momentum of the ball after the collision. This means that the total momentum of the system is conserved, even though the total kinetic energy is not. As a result, the foot and the ball move apart separately after the collision, and the foot does not continue in the same direction as the ball.

Perfectly inelastic collisions

In perfectly inelastic collisions, the two objects stick together after the collision and move together as a single mass. This means that we can treat them as a single object with a total mass equal to the sum of the masses of the two objects.

In terms of momentum, the total momentum of the system before the collision is equal to the total momentum of the system after the collision. This means that the momentum of the two objects before the collision is equal and opposite to the momentum of the combined object after the collision.

Car crashes are often treated as inelastic collisions because the vehicles usually do not bounce off each other and move separately after the collision. Instead, the vehicles may deform and stick together, moving as a single mass. However, energy is lost in the form of heat, sound, and internal energy, making the collision inelastic.

In elastic collisions, both the total momentum and total energy of the system are conserved. However, in inelastic collisions, only the total momentum is conserved while the total energy is not.

Conclusion of collisions

It's important to remember that in real-life situations, collisions are never perfectly elastic or perfectly inelastic. Instead, they are somewhere in between, and we approximate them to either of the extremes to make calculations simpler.

Momentum is a product of mass and velocity, and the higher the momentum, the more force is required to stop an object. Impulse is the force applied over a certain interval of time, and the impulse-momentum theorem states that impulse is the change in momentum. The law of conservation of momentum states that the total momentum before the collision between two objects is the same as the total momentum after the collision.

In elastic collisions, both the total momentum and total energy of the system are conserved. However, in inelastic collisions, only the total momentum is conserved while the total energy is not.

Images

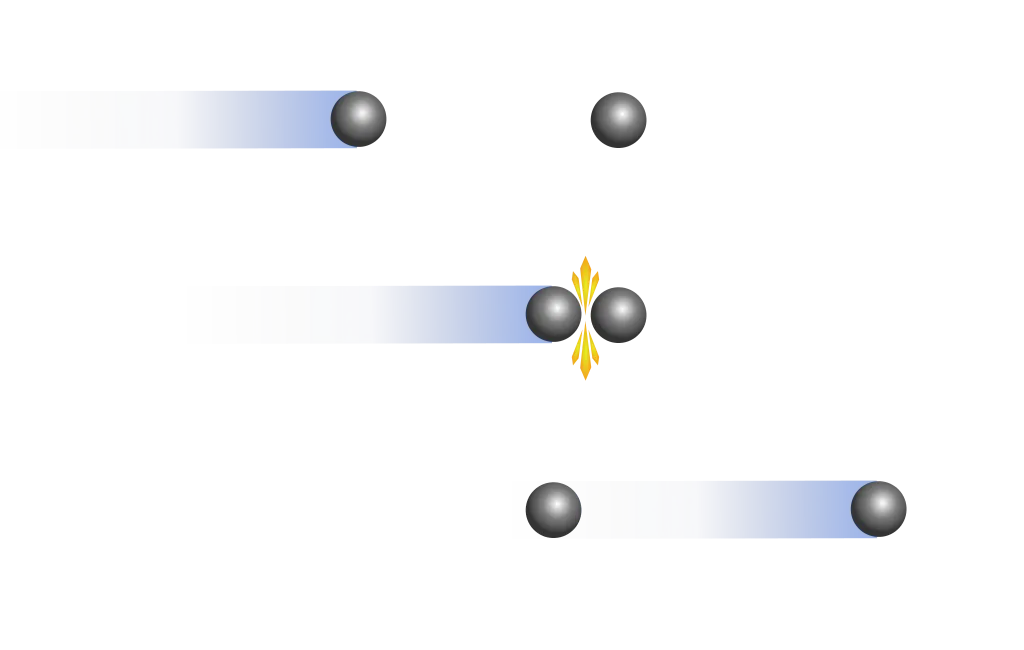
An elastic collision between two particles with the same mass, one of which is at rest.

Momentum

Is inertia momentum?

Inertia is the measure of how much a body can resist motion, whereas momentum is the tendency of a body to keep moving. So, they are not the same. 

What does the momentum of an object mean?

Momentum is a measure of how a body with mass moves with velocity. 

What is the difference between momentum and acceleration?

Momentum is the product of mass and velocity, whereas acceleration is the rate of change of velocity.

‍