Gravitational potential energy is a type of energy that an object has due to its position in a system. Simply put, it's the energy that an object has because of gravity. But how does an object produce this kind of energy? Well, to understand that, we need to what potential. about potential things, mean that they have something inside of them that could lead to greatness. Potential energy is similar - it's the energy stored inside an object because of its position in a system. This energy can come from different sources like electricity, gravity, or elasticity. In this article, we'll focus on gravitational potential energy. We'll also dive into the math behind it and go over a few examples. So let's get started!

Gravitational potential energy definition

Have you ever wondered why a rock dropped from a great height into a pool makes a bigger splash than one dropped from just above the water surface? The answer lies in the concept of gravitational potential energy (GPE). When an object is lifted up in a gravitational field, it gains GPE. This means that the rock dropped from a greater height has more GPE than the one dropped from just above the water surface. GPE is a stored form of energy that is converted into kinetic energy when the object falls.

The amount of GPE an object has depends on its height, the strength of the gravitational field, and its mass. If two objects are lifted to the same height from the surface of the earth and the moon, the object on earth will have more GPE due to the stronger gravitational field.

As the height of an object increases, so does its GPE. When the object falls, its potential energy is converted to kinetic energy, but the total energy remains the same, following the principle of conservation of energy. This principle states that energy can neither be created nor destroyed, only transformed from one type to another.

So, next time you see a big splash in the pool, you'll know it's because the rock had more gravitational potential energy from being dropped from a greater height.

‍

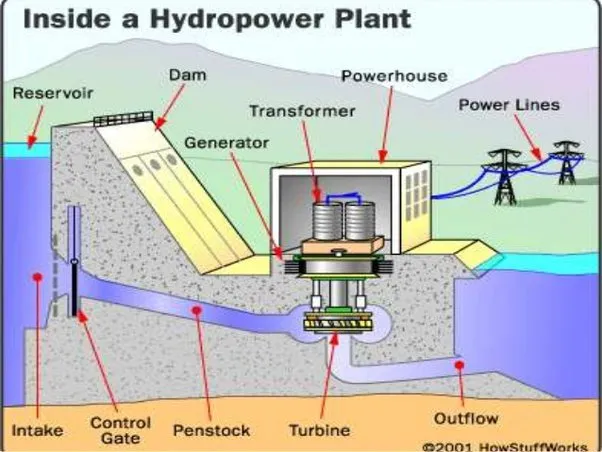
Did you know that water stored on top of a dam can generate electricity? is gravity - always down When the water flows from a height, its gravitational potential energy is transformed into kinetic energy. This kinetic energy can then be harnessed to turn hydroelectric turbines, producing electrical energy.

Just like other types of potential energy, the gravitational potential energy of the water is a stored form of energy. But when the dam is opened, this energy is released and transformed into a different form.

So next time you see a dam, remember that it's not just holding back water - it's also storing potential energy that can be used to power homes and businesses.

Gravitational potential energy formula

The work done to raise an object to a height is equal to the increase in gravitational potential energy. This is due to principle of energy, which states that energy can neither be created nor destroyed, but can be converted from one form to another. Therefore, the work done to raise an object to a height is equal to the increase in gravitational potential energy.

The equation for the gravitational potential energy gained by an object of mass m when it is lifted to a height h in a gravitational field of g is given by:

PEg = mgh

Where PEg is the gravitational potential energy in Joules, m is the mass of the object in kilograms, h is the height in meters, and g is the gravitational field strength on Earth (9.8 m/s2).

Gravitational potential energy examples

Calculate the work done to raise an object of mass to a height of in the earth's gravitational field.  We know that: The gravitational potential energy of the object is now greater, which is also the amount of work done to raise the object. Always make sure that all the units are the same as that in the formula before substituting them.

If a person weighing climbs a flight of stairs to reach a height of then calculate:

(i) Their increase in.

(ii) The work done by the person to climb the flight of stairs.

‍

Using the equation for free fall, we can calculate the speed of the apple when it hits the ground.

v = v₀ + gt

Where v₀ is the initial velocity (0 m/s in this case), g is the gravitational acceleration (9.80665 m/s²) and t is the time taken for the apple to fall (calculated below).

t = √(2h/g)

Where h is the height of the apple (given as 10 m).

Therefore, t = √(2*10/9.80665) = 1.41421356237 s

Substituting this value into the equation for free fall, we get:

v = 0 + 9.80665*1.41421356237 =.8 m/s

‍

The change in potential energy for the frog can using formulaPEWhere m is the mass of frog, g is the acceleration due to gravity, and h is the height of the rock.

∆PE = (0.05 kg) * 9.8 m/s^2 * 0.3 m = 0.147 J

Therefore, the change in potential energy for the frog is 0.147 J.

To calculate the vertical speed at which the frog jumps, we can use the conservation of energy principle, which states that the total energy (kinetic energy + potential energy) of a system is conserved.

At the bottom of the rock, the frog has only kinetic energy, which is given by:

KE = (1/2)mv^2

Where m is the mass of the frog and v is the vertical velocity.

At the top of the jump, the frog has only potential energy, which is given by:

PE = mgh

Where m is the mass of the frog, g is the acceleration due to gravity, and h is the height of the jump.

Since the total energy is conserved, we can equate the kinetic energy at the bottom to the potential energy at the top:

(1/2)mv^2 = mgh

Simplifying the equation, we get:

v = √(2gh)

Plugging in the values, we get:

v = √(2 * 9.8 m/s^2 * 0.3 m) = 1.72 m/s

Therefore, the frog jumps with a vertical speed of 1.72 m/s.

‍

The change in energy of the frog as it makes the leap can be found as follows:

To calculate the vertical speed at take-off, we know that the total energy of the frog at all times is given by:

When the frog is about to jump, it's potential energy is zero, hence the total energy is now

When the frog is  at a height of, then the total energy is in the gravitational potential energy of the frog:

The vertical velocity at the start of the jump can be found by equating theto.

The frog jumps with an initial vertical velocity of.

Gravitational Potential Energy - Key takeaways Work done to raise an object against gravity is equal to the gravitational potential energy gained by the object, measured in joules. Gravitational potential energy is transformed into kinetic energy when an object falls from a height. The potential energy is at a maximum at the highest point and it keeps reducing as the object falls. The potential energy is zero when the object is at ground level. The gravitational potential energy is given by .

Gravitational Potential Energy

What is gravitational potential energy?

Gravitational potential energy is the energy gained when an object is raised by a certain height against an external gravitational field.

What are some examples of gravitational potential energy?

An apple falling from the tree, the working of a hydroelectric dam and the change in speed of a rollercoaster as it goes up and down inclines are a few examples of how gravitational potential energy is converted to velocity as the height of an object changes.

How is gravitational potential energy calculated?

The gravitational potential energy can be calculated using Egpe=mgh

How to find the derivation of gravitational potential energy?

As we know, gravitational potential energy is equal to the work done to raise an object in a gravitational field. Work done is equal to force multiplied by distance (W = F x s ). This can be rewritten in terms of height, mass and gravitational field, such that h = s and F = mg. Therefore, EGPE = W = F x s = mgh.

What is the gravitational potential energy formula?

The gravitational potential energy is given by Egpe=mgh

‍