Angular work and power are important concepts to understand when it comes to objects rotating around an axis. Work is simply a force acting on a body, causing it to move a certain distance. In linear motion, work is calculated by multiplying the force by the distance traveled. In angular motion, however, the work is calculated differently. It's called angular work, and it's the work done by a rotating object to turn around an axis. Angular power, on the other hand, is the power that's delivered to a rotating object. So, whether you're dealing with linear or angular motion, work and power are crucial concepts to get your head around.

Angular work

Angular work is the equivalent of linear work in angular motion. In linear motion, a force is acting on an object, and work is done on it. Similarly, in angular motion, work has to be done to rotate an object about an axis. Work is the result of a torque acting over an angle.

Formula derivation for angular work

When it comes to work done in linear motion, we calculate it by multiplying the force acting on a body with the linear displacement. For angular motion, it's a bit different. We convert the linear displacement into angular displacement using the arc length and radius relationship. Then we determine the angular work done by multiplying the force 'F' with the angular velocity 'θ•r'. It's worth noting that for circular motion, 'T' is to radius 'F•r'. By replacing the torque relation with the angular work equation, we can see that angular work and linear work equations have the same form. In fact, torque is the reciprocal of force in linear work, and angular displacement is the reciprocal of linear displacement. So, just like linear work, angular work is expressed in Joules.

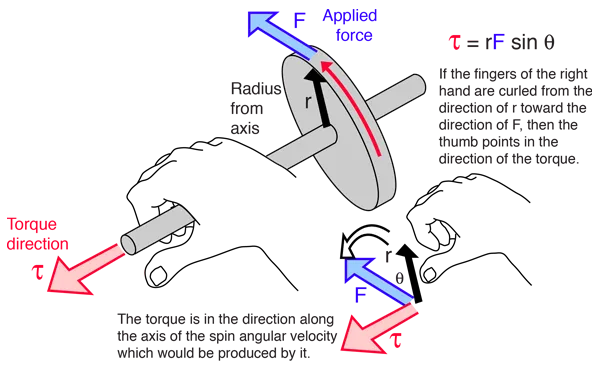
Angular Work and Power: Torque direction

To figure out the direction of torque, we use the right-hand rule. First, we point our fingers towards the direction of rotation, then we extend our thumb upwards. By doing this, our thumb points in a direction perpendicular to the direction of rotation. The direction of the torque is determined by the direction of our thumb (check out figure 1 for a visual).

For vertical rotation, if the direction of rotation is clockwise, the torque is downwards. If it's anticlockwise, the torque is upwards. It's pretty straightforward.

Non-vertical rotation is a bit more complicated, but still easy to figure out. We use the same right-hand rule, but this time, four fingers follow the direction of rotation, while the thumb is extended. The direction of the thumb shows whether the torque is upwards or downwards. Check out figure 2 below for an example.

‍

Angular Work and Power: Work-energy theorem

The work-energy is a fundamental principle that states that the total work done by external forces on a body is equal to the change in its kinetic energy. But to accurately calculate the change in kinetic energy, we must include both the translational kinetic energy (TKe) and the rotational kinetic energy (RKe). The formula for the work-energy theorem is shown below, where W represents work and ΔKe represents the change in kinetic energy:

W = ΔTKe + ΔRKe = ΔKe

By taking into account both the translational and rotational kinetic energies, we can better understand the relationship between work and energy in a physical system. This theorem has important applications in various fields, including physics, engineering, and mechanics.

Angular power

Power is defined as the rate at which energy is being transferred. Linear power is the work done over time. Using the previous relations, we know that the work done for linear motion is equal to the product of the force and its linear displacement. Displacement over time equals velocity.

Formula derivation for angular power

In angular motion, torque is the reciprocal of force in linear motion, while angular velocity is the reciprocal of linear velocity. By substituting angular velocity into the equation, we can express torque as the moment of inertia multiplied by the angular acceleration. We can also modify the work equation to include torque and angular displacement, which gives us a formula for calculating the work done in angular Using the derived work equation, we can also calculate the power needed for the turbine to continue rotating. By substituting torque and angular velocity, we can determine the power required for the turbine to continue rotating.

To determine the work done, we first use the torque equation to calculate torque. We then use the displacement and radius relation to determine the angular displacement in radians. We rearrange the equation to make θ the subject before we substitute the values obtained in the initial work equation.

The key takeaways from this discussion are that angular work is the work done by a torque acting on a body multiplied by the angular displacement, while angular power is the rate of change of energy transfer in angular motion. Rotational dynamics obey the same rules as linear dynamics, as linear formulas have the same form as rotational ones.

Angular Work and Power

What is angular power? 

Angular power is the angular work done over time or alternatively, it is the product of torque and angular rotation as shown in the formula below.Power = (Torque) ⋅ (angular rotation)P = T⋅ ω  

How do you calculate angular work? 

The angular work is calculated with the product of torque and angular displacement as shown in the formula below. Wang= T ⋅  Δ θ 

What is an angular power example?

When a disk is rotating for a period of time and accelerated from its resting position to an initial position, power is the rate at which the disk is rotated and does work.

What is angular work physics? 

The angular work in physics is the net work done on a body to rotate it about a fixed axis. The angular work is equal to the product of torque and the total angular displacement.

‍