When we talk about waves, we use something called "phase" to describe them. Basically, a wave is made up of which go from the highest point (called the crest) to the lowest point (called the trough). A complete cycle is 2π [rad]. But we can also talk about smaller parts of a cycle, like half or a quarter. These are measured in radians, which don't have any units. So, when we talk about phase, we're really just talking about how much of a cycle we're looking at.
![Wave cycles are divided into radians, with each cycle covering 2π [rad] of distance. Cycles repeat after 2π [rad] (red values)](https://assets-global.website-files.com/625e75c5d17b9b8f0220b7bb/63fca0e9ba5ade95c7ff3069_Phasor_Diagram_Sinusoidal_Waveform.jpeg)
If you want to figure out the phase of a wave in a certain spot, you need to know how far that spot is from the start of the wave cycle. Let's say your wave is a simple up-and-down shape like a sine or cosine function. The equation for this type of wave looks like: A is the biggest height of the wave, x is a value on the horizontal line that goes from 0 to 2π, and y is the height of the wave at that point. To find the phase of any point on the wave, you use this formula: This formula gives you the value of x in radians, but we usually use degrees instead. To convert, you just multiply x by 180 and then divide by π. Sometimes, a wave can be described by a different equation that's not quite in sync with a regular sine or cosine wave. In these cases, the wave might be out of phase by a certain amount.
The phase difference of waves occurs when two waves move and their cycles do not coincide. The phase difference is known as the cycle difference between two waves at the same point.
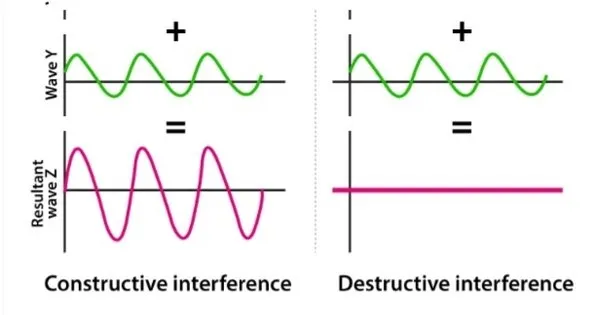
Overlapping waves that have the same cycle are known as waves in phase, while waves with phase differences that do not overlap are known as out of phase waves. Waves that are out of phase can cancel each other out, while waves in phase can amplify each other.
If two waves have the same frequency/period, we can calculate their phase difference. We will need to calculate the difference in radians between the two crests that are next to each other, as in the following figure.
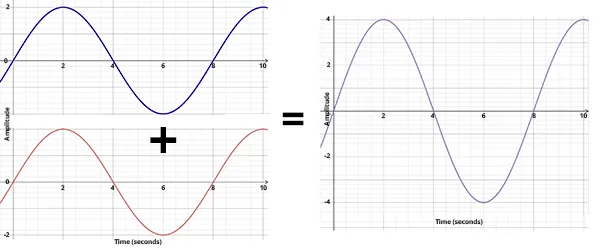
This difference is the phase difference:
Here is an example of how to calculate the wave phase and the wave phase difference.
A wave with a maximum amplitude A of 2 metres is represented by a sine function. Calculate the wave phase when the wave has an amplitude of y = 1.
Using the y = A • Sin (x) relationship and solving for x gives us the following equation:
This gives us:
Converting the result to radians, we get:
Now let’s say another wave with the same frequency and amplitude is out of phase with the first wave, with its phase at the same point x being equal to 15 degrees. What is the phase difference between the two?
First, we need to calculate the phase in radians for 15 degrees.
Subtracting both phases, we obtain the phase difference:
In this case, we can see that the waves are out of phase by π / 12, which is 15 degrees.
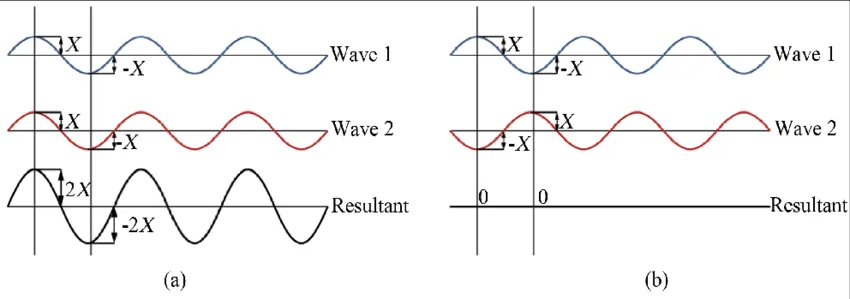
When waves are in phase, their crests and troughs coincide with each other, as shown in figure 3. Waves in phase experience constructive interference. If they vary in time (i(t) and u(t)), they combine their intensity (right: purple).
Phase difference can have different effects depending on the type of wave, and these effects can be used in many practical applications. One example is seismic technology, which uses spring-mass systems to counteract the movement of seismic waves. This is especially important for tall buildings like the Taipei 101 tower. In the image provided, you can see a huge sphere hanging from the top of the tower. This sphere is actually a pendulum with a weight of 660 metric tons! When the building experiences strong winds or seismic waves, the pendulum swings back and forth, moving in the opposite direction to the building's movement. This helps to stabilize the tower and keep it from swaying too much.
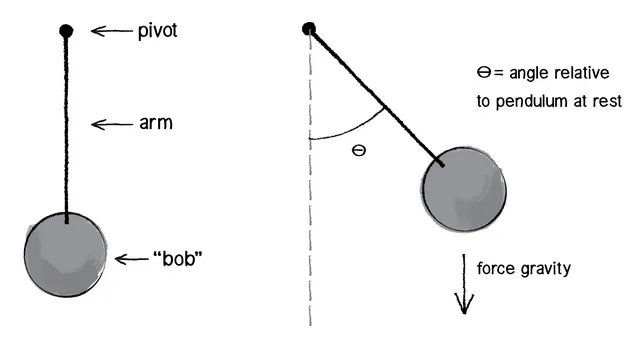
The huge pendulum in the Taipei 101 tower has multiple purposes. Not only does it reduce the oscillations of the building, but it also dissipates the energy, acting as a tuned mass damper. In 2015, a typhoon hit the tower, causing the pendulum ball to swing more than a meter, which demonstrates its effectiveness in mitigating the impact of strong winds and seismic waves.
To summarise, the phase difference is a value that represents a fraction of a wave cycle. Waves that are in phase overlap and create a constructive interference that increases their maximums and minimums. However, when waves are out of phase, they create a destructive interference, which can produce irregular patterns. In extreme cases, when the waves are out of phase by 180 degrees but have the same amplitude, they cancel each other out.
The concept of phase difference has been used to create technologies for seismic mitigation and sound-cancelling technologies.
How do you calculate phase difference?
To calculate the phase difference between two waves with the same period and frequency, we need to calculate their phases at the same point and subtract the two values.Δφ = φ1-φ2
What is phase difference?
Phase difference is the cycle difference between two waves at the same point.
What does a phase difference of 180 mean?
It means that the waves have a destructive interference and thus cancel each other out if they posses the same intensity.
What is meant by phase?
The phase of a wave is the value representing the fraction of a wave cycle.
