Have you ever wondered how Einstein's Theory of Special Relativity works? It's a fascinating concept that explains how mass, time, and space are affected by speed. Let's break it down and explain it in simple terms.

First, let's talk about inertial frames of reference. This is a reference frame where a body at rest remains at rest and a body in motion continues at a constant speed in a straight line unless impacted by an outside force. This is similar to Newton's first law of motion. For example, if you're in a car driving on a road, the motion of the car is measured relative to the road. Or if you throw a ball off a large cliff, the motion of the ball is measured relative to your standing point.

The laws of physics are the same in all inertial frames of reference, and they can be stated in much simpler forms than in non-inertial frames. For example, when you're in the back seat of a car going at a constant speed, the laws of physics appear to work the same way as when you're standing on the surface of the earth. But when the car is moving, things get a bit more complicated.

Einstein's second postulate of the theory of special relativity is about the speed of light, which is a constant independent of the reference frame. This means that in a vacuum, the speed of light is always the same at c = 3.00 ⋅ 10^8 m/s.

Time intervals and the distance traveled can be different from one observer to another. For example, the elapsed time of an exam is the same for all students, but at relativistic speeds, the observer's relative velocity and the event being observed can affect the elapsed time.

‍

Time dilation

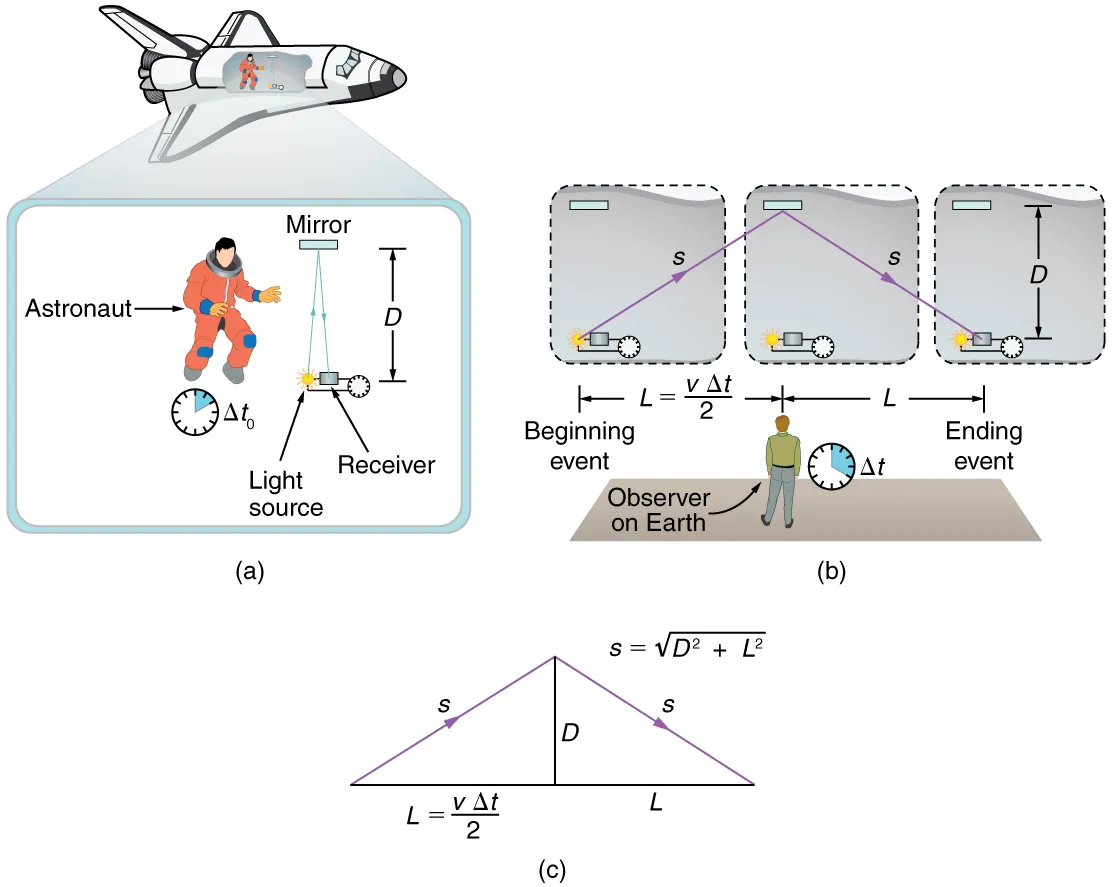
It's a fascinating concept that's a consequence of Einstein's Theory of Special Relativity. In simple terms, time dilation refers to the fact that time moves slower for objects that are moving at high speeds or in strong gravitational fields.

This may sound strange, but it's been proven with experiments. For example, if you were to observe a clock that's moving at a high speed, you would notice that it appears to be ticking slower than a clock that's stationary. Similarly, if you were to observe a clock in a strong gravitational field, such as near a black hole, you would also notice that it appears to be ticking slower than a clock outside of the gravitational field.

The reason for this is that time and space are not separate and independent, but are actually part of a single four-dimensional space-time. This means that time and space are intertwined and can be affected by motion and gravity.

This concept has important implications for space travel and our understanding of the universe. For example, time dilation means that astronauts who travel at high speeds or in strong gravitational fields will experience time differently than people on Earth. This can lead to interesting effects such as the "twin paradox," where one twin who travels in space at high speeds will age slower than the other twin who stays on Earth.

Overall, time dilation is a mind-bending concept that challenges our understanding of time and space. But it's also a concept that has been proven with experiments and has important implications for our understanding of the universe. 

Length contraction

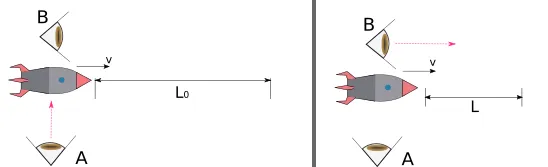
When traveling at everyday speeds, observers can and will measure the length of a car journey the same, always independently of the velocity observers are traveling at. But that does not apply under relativistic speeds, which are close to the speed of light.

Let's imagine a spaceship is observed by someone on Earth and travels at a velocity of 0.750c for 9.05µs from the moment it is spotted until it vanishes. It covers the following distance:

‍

This is relative to Earth. In the spaceship's frame of reference, its lifetime is Δt0:In the question, it says 'to an observer on Earth' so 9.05µs is Δt and you need Δt0 to find the length from the spaceship's reference. As we saw before:

Finally, the distance between when the spaceship appears and when it vanishes, is determined by who is measuring it and how the observer moves relative to it.

While the distances are observed the same by all observers in everyday life, they can be observed differently in relativistic speeds.

What is relativistic energy?

The law of the conservation of energy states that energy has many forms, and each form can be converted to another without being destroyed; the energy in a system remains constant.

Total energy

Total energy E can be defined as

m is mass in kg.

c is the speed of light in m / s.

As you may remember we defined  as:

v, is velocity in m / s.

Rest energy

Have you ever heard of Einstein's famous equation, E=mc²? It's a fundamental concept in physics that demonstrates the relationship between energy and mass. In simple terms, it means that when energy is stored in an object its mass increases. It also suggests that mass can be destroyed to release energy.

Let's look at an example to understand this concept better. If we want to calculate the rest energy of a 1-gram mass, we can use the equation E=mc². We know that 1 gram is equal to 1⋅10^-3 kg, so we can substitute that into the equation. The result is an enormous amount of energy, about twice the amount released by the Hiroshima atomic bomb.

Both the Sun and nuclear power plants convert mass into energy through nuclear fusion and fission, respectively. This concept has important implications for our understanding of energy and the universe.

Einstein's Theory of Special Relativity also includes other key concepts, such as reference frames, the speed of light, length contraction, and time dilation. These concepts are all related to how time, speed, and space interact, and how the laws of physics are the same in all inertial frames.

Overall, Einstein's Theory of Special Relativity is a fundamental concept in physics that challenges our understanding of the universe. But it's also a concept that has been proven with experiments and has important implications for our understanding of energy, mass, and the laws of physics.

Einstein's Theory of Special Relativity

What does Einstein’s theory of special relativity tell us?

Einstein’s theory of special relativity tells us that the laws of physics are the same in all inertial frames of reference and that the speed of light in a vacuum is constant regardless of the motion of the observer.

What are the two postulates of Einstein’s theory of special relativity?

The first postulate of Einstein’s theory of special relativity states that the laws of physics are the same in all inertial frames of reference. The second postulate states that in a vacuum, the speed of light is constant at  c=3.00*10^8 m/s. 

How can we explain Einstein’s theory of special relativity?

According to special relativity, the speed of light is a limit that can be approximated but never exceeded by any object with mass. It is the source of one of the most famous equations in science, E=mc^2, which states that mass and energy are the same physical entity and can be transformed into one another.

‍