Gravitational potential is a special type of force field that conserves energy along with closed loops in the field. When a body leaves and returns to a certain point in space, the net energy doing so is is with a spatial.

To put it simply, gravitational potential is the energy needed to move an object to a location from a fixed reference position in a gravitational field. This energy is related to the principle of stability, which states that objects tend to have the lowest energy possible.

To find the force associated with a potential, we can differentiate it. The full mathematical description of this process is beyond the scope of this article. Understanding gravitational potential is essential in describing the dynamics of objects that are subject to a certain field.

Mathematical description of gravitational potential energy

Gravitational energy holds a lot of valuable information about the nature of gravity and its role in our world. By comprehending this energy, we can gain a better understanding of the physical properties of gravity.

Equations of gravitational potential energy

Newton's law of gravitation offers a simple way to describe gravity, despite not being the most accurate theory. This description of gravity is characterized by its spherical symmetry, meaning there are no special spatial directions.

The formula for the gravitational field strength includes the gravitational force vector Z, the mass of the body M, the radial distance to the source body r, the unit radial vector er, and the universal constant of gravitation G. This formula allows us to calculate the gravitational field strength.

The expression for the gravitational potential energy is also based on spherical symmetry. All points at a constant distance from the source body have the same gravitational potential energy. This means that all bodies on the surface of the earth have the same gravitational potential energy.

By differentiating the expression for gravitational potential energy with respect to radial distance r, we can obtain the formula for gravitational field strength. These expressions help us understand the fields produced by a mass M. If we want to know the force experienced by a mass m under the gravitational field or its gravitational potential energy, we can simply multiply the expressions by a factor m.

Gravitational potential: energetic considerations

To understand the concept of gravitational potential energy, we first analyse its units. By multiplying the mass of an object m with the expression for gravitational potential energy, we get the units of energy, which are Joules. This is why it is called gravitational potential energy.

The principle of stability states that objects tend to minimize their energy. In the case of gravitational potential energy, this means that objects will tend to reduce their radial distance from the source body, as indicated by the negative sign in the expression for gravitational potential energy. The following graph can help us to understand this concept better.

‍

‍

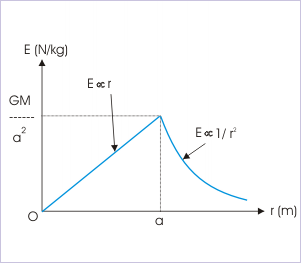
The graph shows that the gravitational potential energy decreases as the radial distance from the source body decreases. The force experienced by an object can be calculated by taking the derivative of the gravitational potential energy. The slope of the tangent line at each point corresponds to the magnitude of the gravitational force.

As the radial increases, the slope of the tangent line decreases, eventually reaching zero at an infinite radial distance. At this point, the gravitational potential energy becomes zero, indicating that the object is no longer under the influence of the gravitational field.

How to solve gravitational potential energy examples

When dealing with spatial distributions, it is common to use graphs that involve the field equations without including the test mass m. When considering specific values for a mass m, we need to use the other two equations, remembering that U represents the potential energy of an object entering the total energy formula with a minus sign.

Let's consider a scenario where we have a body with a mass M of 1.50 x 10^10 kg, and we place a body with a mass m of 1.00 kg to observe its behavior under the gravitational field created by the body with mass M. Since mass m has the unit mass, the numerical value of the gravitational field and the gravitational force, as well as the numerical value of the gravitational potential field and gravitational potential energy, will be the same. However, these are different concepts with different units.

We can compute all the functions and study their behavior. For the gravitational potential energy, we get a graph similar to the one in figure 1. For the gravitational force, we can represent its magnitude as a function of the radial distance r, ignoring the radial space orientation, which would require a complex graph.

‍

‍

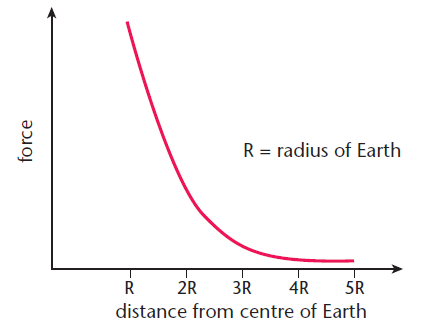
As we analyze the behavior of the gravitational force and energy in relation to the radial distance, we can observe that both of these quantities approach zero as we move towards infinite radial distance. This is logical since there should not be any gravitational influence between two objects if they are infinitely separated, and the energy associated with the field should be zero.

However, as we move towards a null radial distance, we can see that both the strength of the force and the energy diverge. This divergence signals that Newton's law is not valid in such circumstances.

When considering spheres centered on the gravitational source, we observe that neither the strength of the force nor the energy changes. Although the direction of the force changes as it is directed towards the center/source, the strength of the force and energy remain the same. This is why we do not experience changes in the strength of gravity when moving around on the earth's almost spherical surface. We do not need to put energy into doing so unless we go upwards, like climbing a mountain, where we gain energy. Conversely, when we go down an inclined surface, we lose energy, which is why it does not cost us any effort. Many extreme sports are based on this principle.

Gravitational potential approximation on the surface of a planet

The formula for objects close to the surface of the earth provides an approximation that simplifies the calculation of gravitational potential energy. It shifts the zero energy, which is located at an infinite radial distance, to the surface of the earth.

The formula for gravitational potential energy for objects close to the surface of the earth is given by:

E = mgh

Here, E is the gravitational potential energy, m is the mass of the body, g is the gravitational surface acceleration for the earth (equal to G·M / R2 = 9.81 m/s2), and h is the height over the surface of the earth.

The gravitational force is a field, and we can associate energy with it. The gravitational field is conservative, meaning its energy is conserved in closed loops, and there is a function called gravitational potential that captures the information about the field and its energy. The gravitational potential energy is spherically symmetric and thus depends only on the radial distance. There are approximations for certain regimes to compute the gravitational potential energy, such as the formula for objects close to the earth’s surface.

Gravitational Potential

How to calculate the gravitational potential energy?

We can apply the formula (-G⋅m⋅M) / r for the general expression based on Newton’s law or use the approximation m⋅g⋅h for objects close to the earth’s surface.

What units are used for the gravitational potential energy?

Joules are the units used to measure energy. It is equivalent to kg⋅m2/s2.

Why is the gravitational potential energy negative?

It is negative because the minus sign is necessary to capture the attractive character of the gravitational force.

What is gravitational potential energy?

It is the energy a body with mass has because of the presence of a gravitational field.

‍