Gases are a type of system that moves randomly and doesn't lose much energy when interacting with other particles. They're easy to study and have simple math rules. Scientists made great discoveries about gases in the 17th-19th centuries. They found laws that connect the pressure, volume, and temperature of a gas under certain conditions. These laws are called 'Ideal gas laws' and come from a theoretical model called 'Ideal gas model'. This model links the microscopic particles that make up gases with the larger properties like temperature. Understanding this connection is important for understanding ideal gas laws.

What is kinetic molecular theory?

The kinetic molecular theory studies matter as a system of many particles. It focuses on the movement of these particles to understand the properties of the system. The word 'kinetic' refers to this emphasis on movement when studying microscopic particles.

Main quantities

Kinetic molecular theory focuses on four main quantities when studying matter. The first is position, which helps determine whether a system is in a solid, liquid, or gas state. The second is speed, which is used to determine pressure and temperature. The third is kinetic energy, which comes in many forms and is relevant in different ways for different phases of matter. Lastly, there is interaction/potential energy, which captures how particles in a sample of matter interact with each other. In gases, this energy is not very important, but in solids, it is the main source of energy that keeps particles close together.

Macroscopic interpretation

In thermodynamics, we study macroscopical quantities that are related to the microscopical quantities of kinetic molecular theory. Temperature a measure of the average kinetic energy of particles in a system, which determines how quickly particles move around and how much vibrational energy they have. Pressure is a measure of the force per unit of area that particles exert on the boundaries of the space they occupy, which is related to the distribution of kinetic energy and informs the distribution of this energy. Volume is a measure of the space particles occupy and is closely related to the spacing between particles, which influences the strength of interactions and varies from one phase to another. Total energy is a global measure that takes into account both the kinetic and potential energy of particles and their distribution throughout the sample.

What is the relevance of ideal gases?

The ideal gas model is a useful approximation because it simplifies the behavior of real gases by assuming that the molecules occupy no volume and do not interact with each other. This allows us to derive simple equations that relate the macroscopical thermodynamic quantities of pressure, volume, and temperature. However, the ideal gas model fails to accurately describe the behavior of real gases under certain conditions, such as at high

Assumptions of the model

The model of ideal gases is a very useful approximation to understand the behaviour of real gases. It is based on several assumptions derived from the microscopic kinetic molecular theory. These assumptions include that there are no intermolecular forces, that collisions among particles are brief, elastic, and random, and that particles have no volume, among others. These properties allow us to study macroscopic quantities like,. movement particles the use of averages to define these quantities, while Newton us to study the transfer of momentum between particles and their boundaries. Additionally, the elasticity of collisions implies that the kinetic energy of ideal gases is conserved, which is equal to the total energy because there is no potential energy due to the lack of intermolecular forces. However, it is essential to understand that this model is an approximation, and under certain conditions, it may fail, requiring the use of more complex models to understand the behaviour of real gases.

Law of ideal gases

The law of ideal gases is an equation that captures the relationship between the three main macroscopical quantities: pressure, temperature, and volume. It also includes the particle content of the system under study through the use of the number of mols, or n. The equation is shown below.

where P is the pressure of the gas, V is the volume, T is the temperature (in Kelvin) and R is the ideal gas constant (with an approximate value of 8.31 J / mol·K ).

This equation can be derived for n moles of particles that behave according to the assumptions listed before, and by performing statistical analysis to extract thermodynamical quantities. From this equation, leaving the particle content and one of the thermodynamical quantities fixed, one can arrive at the three laws of ideal gases:

‍

Applicability

The ideal gas law is a powerful tool to understand the behaviour of gases. However, it is important to note that this model is an approximation and may not hold under certain conditions. Two main reasons for this are the volume of gas particles and intermolecular forces between them. The Van der Waals equation takes these factors into account with parameters 'a' and 'b', and reduces to the ideal gas law when these parameters are set to 0. The ideal gas law holds for a situation where the molar volume of the substance is much larger than 'a' and 'b'. In this case, even though the particles have volume and there are intermolecular forces between them, they are negligible compared to the large volume available to the substance. As a result, the intermolecular forces between particles can be considered approximately zero. Understanding the limitations of the ideal gas law is crucial when studying the behaviour of gases under different conditions.

‍

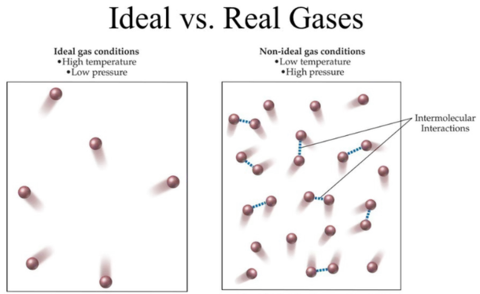
Ideal Gases - Key takeaways

The ideal gas model is a simplified model that assumes that gas particles are infinitely small and do not interact with each other. The kinetic molecular theory provides a more detailed framework for studying many-particle systems, such as gases, and extracting thermodynamic quantities through statistical techniques. This theory assumes elastic collisions and no potential energy between particles. However, gases in the real world do not always behave in accordance with the ideal gas model due to intermolecular forces and non-zero particle size. The Van der Waals equation takes these deviations into account by introducing parameters that quantify the strength of intermolecular forces and the size of gas particles. By considering these factors, the Van der Waals equation provides a more accurate description of gas behavior than the ideal gas law.

Ideal Gases

How do real gases differ from ideal gases?

Real gases are not made of point-like particles, and there are intermolecular forces present.

Do gases always follow the ideal gas law?

No, they can be described by this law under certain thermodynamic conditions that match the assumptions of the ideal gas model.

Do ideal gases exist?

They do not exist as universal systems, but they describe the behaviour of gases within a certain regime of thermodynamic conditions.

‍